个人技术笔记

Hopfield神经网络（Hopfield Nets）

发布时间：2016-02-12  栏目：深度学习  评论：0 Comments

 

 

 

1982年，J．Hopfield提出了可用作联想存储器的互连网络，这个网络称为Hopfield网络模型，也称Hopfield模型。Hopfield神经网络模型是一种循环神经网络，从输出到输入有反馈连接。Hopfield网络有离散型和连续型两种。

反馈神经网络由于其输出端有反馈到其输入端；所以，Hopfield网络在输入的激励下，会产生不断的状态变化。当有输入之后，可以求取出Hopfield的输出，这个输出反馈到输入从而产生新的输出，这个反馈过程一直进行下去。如果Hopfield网络是一个能收敛的稳定网络，则这个反馈与迭代的计算过程所产生的变化越来越小，一旦到达了稳定平衡状态；那么Hopfield网络就会输出一个稳定的恒值。对于一个Hopfield网络来说，关键是在于确定它在稳定条件下的权系数。

应该指出：反馈网络有稳定的，也有不稳定的。对于Hopfield网络来说，还存在如何判别它是稳定网络，亦或是不稳定的问题；而判别依据是什么，也是需要确定的。

1．3．1 离散Hopfield网络

Hopfield最早提出的网络是二值神经网络，神经元的输出只取1和0这两个值，所以，也称离散Hopfield神经网络。在离散HopfieId网络中，所采用的神经元是二值神经元；故而，所输出的离散值1和0分别表示神经元处于激活和抑制状态。

首先考虑由三个神经元组成的离散Hopfield神经网络，其结构如图1—13中所示。

在图中，第0层仅仅是作为网络的输人，它不是实际神经元，所以无计算功能；而第一层是实际神经元，故而执行对输人信息和权系数乘积求累加和，并由非线性函数f处理后产生输出信息。f是一个简单的阀值函效，如果神经元的输出信息大于阀值θ，那么，神经元的输出就取值为1；小于阀值θ，则神经元的输出就取值为θ。

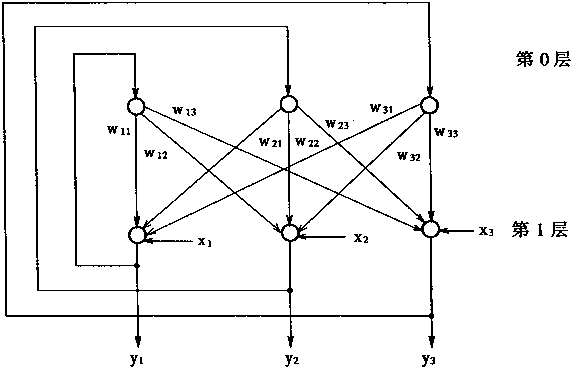
图1-13  三神经元组成的Hopfield网络

对于二值神经元，它的计算公式如下

其中：x_i为外部输入。并且有：

Y_i=1,当U_i≥θ_i时

Y_i=0,当U_i<θ_i时

对于一个离散的Hopfield网络，其网络状态是输出神经元信息的集合。对于一个输出层是n个神经元的网络，则其t时刻的状态为一个n维向量：

Y(t)=[Y₁(t),Y₂(t),^…,Y_n(t)]^T

故而，网络状态有2ⁿ个状态；因为Yj(t)(j＝1……n)可以取值为1或0；故n维向量Y(t)有2ⁿ种状态，即是网络状态。

对于三个神经元的离散Hopfield网络，它的输出层就是三位二进制数；每一个三位二进制数就是一种网络状态，从而共有8个网络状态。这些网络状态如图1—14中所示。在图中，立方体的每一个顶角表示一种网络状态。同理，对于n个神经元的输出层，它有2ⁿ个网络状态，也和一个n维超立方体的顶角相对应。

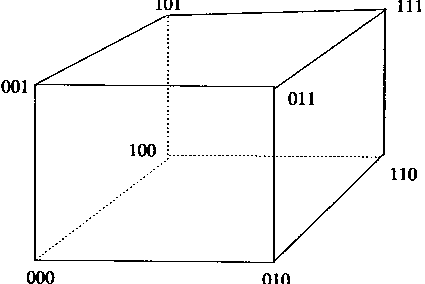
图1-14   三神经元输出层的网络状态

如果Hopfield网络是一个稳定网络，那么在网络的输入端加入一个输入向量，则网络的状态会产生变化，也就是从超立方体的一个顶角转移向另一个顶角，并且最终稳定于一个特定的顶角。

对于一个由n个神经元组成的离散Hopfield网络，则有n*n权系数矩阵w：

W={W_ij} i=1,2,^…,n  j=1,2,^…,n

同时，有n维阀值向量θ：

θ=[θ₁,θ₂,^…θ_n]^T

一船而言，w和θ可以确定一个唯一的离散Hopfield网络。对于图1—13所示的三神经元组成的Hopfield网络，也可以改用图1—15所示的图形表示，这两个图形的意义是一样的。考虑离散Hopfield网络的一船节点状态；用Y_j(t)表示第j个神经元，即节点j在时刻t的状态，则节点的下一个时刻(t+1)的状态可以求出如下：

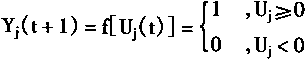
当W_ij在i＝j时等于0，则说明一个神经元的输出并不会反馈到它自己的输入；这时，离教的HopfieId网络称为无自反馈网络。

当W_ij在i＝j时不等于0，则说明—个神经元的输出会反馈到它自己的输入；这时，离散的Hopfield网络称为有自反馈的网络。

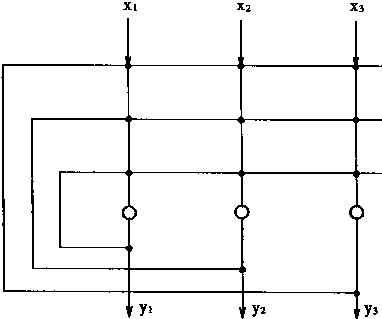
图1-15 离散Hopfield网络的另外一种图示 离散Hopfield网络有二种不同的工作方式：

1．串行(异步)方式

在时刻t时，只有某一个神经元j的状态产生变化，而其它n-1个神经元的状态不变这时称串行工作方式。并且有

Y_i(t+1)=Y_j(t)  i≠j

在不考虑外部输人时，则有

2．并行(同步)方式

在任一时刻t，所有的神经元的状态都产生了变化；则称并行工作方式。并且有

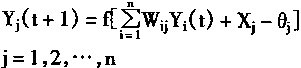
在不考虑外部输入时，则有

    j=1,2,^…,n

对于一个网络来说，稳定性是一个重大的性能指标。

对于离散Hopfield网络，其状态为Y(t)：

Y(t)=[Y₁(t),Y₂(t),^…,Y_n(t)]^T

如果，对于任何△t>0．当神经网络从t＝0开始，有初始状态Y(0)；经过有限时刻t，有：

Y(t+△t)=Y(t)

则称网络是稳定的。

在串行方式下的稳定性称之为串行稳定性。同理，在并行方式的稳定性称之为并行稳定性。在神经网络稳定时，其状态称稳定状态。

从离散的Hopfield网络可以看出：它是一种多输入，含有阀值的二值非线性动力系统。在动力系统中，平衡稳定状态可以理解为系统的某种形式的能量函数在系统运动过程中，其能量值不断减小，最后处于最小值。

对Hopfield网络引入一个Lyapunov函数，即所谓能量函数：

即有：

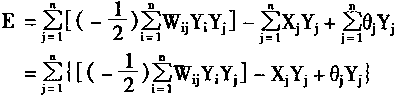	(1-46)
对于神经元j，其能量函数可表示为
	(1-47)

也即是有

神经元j的能量变化量表示为△E_j：

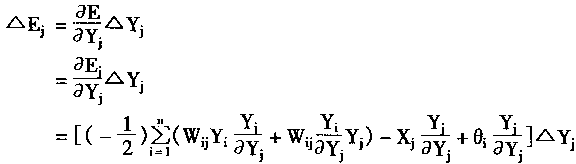(1-48)

如果存在条件   W_ii=0,i=1,2,…,n

W_ij=W_ji  i=1,2,…,n   j=1,2,…,n

则有：

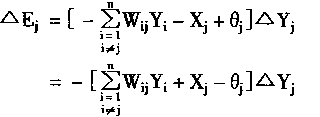(1-49)

其中：E_j为神经元j的能量；

△E_j为神经元j的能量变化；

W_ij为神经元i到神经元j的权系数：

Y_i为神经元j的输出；

X_j为神经元j的外部输入；

θ_j为神经元j的阀值；

△Y_j为神经元j的输出变化。

如果，令

U_j=ΣW_ijY_i+X_j

则△E_j可表示为：

考虑如下两种情况：

1．如果U_j≥θ_j，即神经元j的输入结果的值大于阀值，则U_j–θ_j≥0，则从二值神经元的计算公式知道：Y_j的值保持为1，或者从0变到1。这说明Y_j的变化△Y_j只能是0或正值。这时很明显有△E_j：

△E_j≤0

这说明Hopfield网络神经元的能量减少或不变。

2．如果U_j≤θ_j，即神经元j的输入结果的值小于阀值，则U_j–θ_j≥0，则从二值神经元的计算公式可知：Y_j的值保持为0，或者从1变到0。这说明Y_j的变化△Y_j只能是零或负位。这时则有△E_j：

△E_j≤0

这也说明Hopfield网络神经元的能量减少。

上面两点说明了Hopfield网络在权系数矩阵W的对角线元素为0，而且W矩阵元素对称时，Hopfield网络是稳定的。

Coben和Grossberg在1983年给出了关于Hopfield网络稳定的充分条件，他们指出：

如果Hopfield网络的权系数矩阵w是一个对称矩阵，并且，对角线元素为0．则这个网络是稳定的。即是说在权系数矩阵W中，如果

i=j时，W_ij=0

i≠j时，W_ij=W_ji

则Hopfield网络是稳定的。

应该指出：这只是Hopfield网络稳定的充分条件．而不是必要条件。在实际中有很多稳定的Hopfield网络，但是它们并不满足权系数矩阵w是对称矩阵这一条件。

上面的分析可知：

无自反馈的权系数对称Hopfield网络是稳定的网络。它如图1—16，图1—17所示。

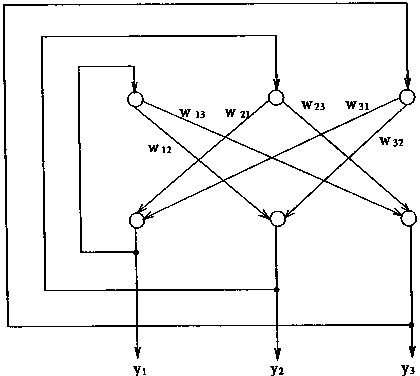
图1-16  对角线权系数为0的对称Hopfield网络

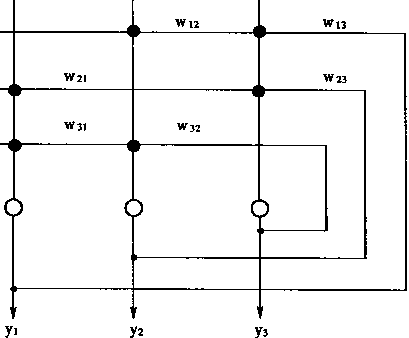
图1-17  对角线权系数为0的对称网另一图示

Hopfield网络的一个功能是可用于联想记忆，也即是联想存储器。这是人类的智能特点之一。人类的所谓“触景生情”就是见到一些类同过去接触的景物，容易产生对过去情景的回昧和思忆。对于Hopfield网络，用它作联想记忆时，首先通过一个学习训练过程确定网络中的权系数，使所记忆的信息在网络的n维超立方体的某一个顶角的能量最小。当网络的权系数确定之后，只要向网络给出输入向量，这个向量可能是局部数据．即不完全或部分不正确的数据，但是网络仍然产生所记忆的信息的完整输出。1984年Hopfield开发了一种用n维Hopfield网络作联想存储器的结构。在这个网络中，权系数的赋值规则为存储向量的外积存储规则(out product storage prescription)，其原理如下：

设有m个样本存储向量x₁，x₂，…，x_m

X_1={X_11,X_21,…_,X_m1}

X_2={X_12,X_22,…,X_m2}

_……

X_m={X_m1,X_m2,…,X_mm}

把这m个样本向量存储人Hopfield网络中，则在网络中第i，j两个节点之间权系数的值为：

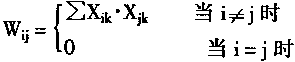
其中：k为样本向量X_k的下标，k＝1，2，…m；

i，j分别是样本向量X_k的第i，j分量X_i，X_j的下标；i，j＝1，2，…n。

对联想存储器的联想检索过程如下：

给定一个向量X。进行联想检索求取在网络中的存储内容。这时，把向量

X={X₁,X₂,…X_n}

的各个分量x₁，x₂，…，x_n赋于相对应的节点j，(j＝1，2，…，n)，则节点有相应的初始状态Y_j(0)，则有

Y_j(0)=X_j，j＝1，2，…，n

接着，在Hopfield网络中按动力学系统原则进行计算，得

Y_j(t+1)=f[ΣW_ijY_j(0)-θ_j]  , i,j＝1，2，…，n

其中，f[·]是非线性函数，可取阶跃函数。

通过状态不断变化，最后状态会稳定下来．最终的状态是和给定向量x最接近的样本向量。所以，Hopfield网络的最终输出也就是给定向量联想检索结果。这个过程说明，即使给定向量并不完全或部分不正确，也能找到正确的结果。在本质上，它也有滤波功能。

1．3．2连续Hopfield网络

连续Hopfield网络的拓朴结构和离散Hopfield网络的结构相同。这种拓朴结构和生物的神经系统中大量存在的神经反馈回路是相一致的。在连续Hopfield网络中，和离散Hopfield网络一样，其稳定条件也要求W_ij=W_ji。
连续Hopfield网络和离散Hopfield网络不同的地方在于其函数g不是阶跃函数，而是S形的连续函数。一般取

g(u)=1/(1+e^-u)        (1-50)

连续Hopfield网络在时间上是连续的．所以，网络中各神经元是处于同步方式工作的。考虑对于一个神经细胞，即神经元j，其内部膜电位状态用u_j表示．细胞膜输入电容为C_j，细胞膜的传递电阻为R_j，输出电压为V_j，外部输入电流用I_j表示，则连续Hopfield网络可用图1—18所示的电路表示。

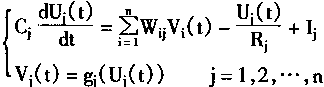(1-51)

其中：n是神经网络神经元的个数

v_j(t)为输出电位；

U_j(t)为输入电位。

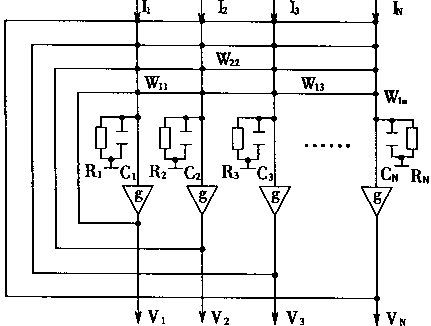
图1-18  连续Hopfield网络的电路形式

对于连续Hopfield网络，Hopfield给出如下稳定性定理：

给出能量函数E(t)

(1-52)

其中：g^-1(v)是V_j(t)＝g_j(u_j(t))的反函数。

如果连续Hopfield网络中神经元传递函数是单调增长的连续并有界函数，并且W_ij＝W_ji，则有

当并且仅当

时，有

这个定理的意义可以解释如下：当网络神经元的传递函数是S函数，并且网络权系数矩阵对称；则随时间的变化网络的能量会下降或不变；而且仅当输出电位随时间变化不变时．网络的能量才会不变。换而言之，在上述条件下的网络是能量不变或下降的。

这个定理的证明过程如下：

对能量函数E(t)求时间的导数dE(t)／dt，则有

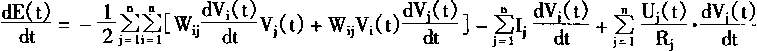(1-53)

如果存在Wij＝Wji，则上式可写为

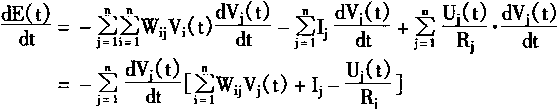	(1-54)
从连续Hopfield网络的动态方程，有
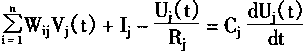	(1-55)
故上面(1—54)式可写成
	(1-56)
由于  Vj(t)=gj(Uj(t))	(1-57)
故而有  Uj(t)=gj-1(Vj(t))	(1-58)
从而有
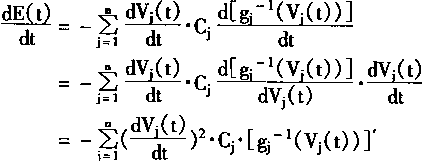	(1-59)
从   g(u)=1/(1+exp(-u))	(1-60)

可知其反函数为单调升函数。因而对于dE(t)／dt中的g_j^-1(v_j(t))，必有单调升的特点．则其导数必定大于0，即

[g_j^-1(v_j(t))]’>0

同时容易知道

C_j>0

很明显，在dE(t)／dt时，必定有

而且当，仅当

有

至此，则定理证明完毕。

这个定理说明Hopfield网络的能量函数E(t)是单调下降的；如果E(t)有下界，即有确定的极小值；那么网络必定是稳定的。而且，可以知道稳定点对应于能量函数的下界，即极小值。

下一步工作，只需证明能量函数有下界，那么．就可以证明网络是稳定的。

可以证明，如果Hopfield网络的传递函数g是连续而且有界的，那么，能量函数E(t)是有界的。

最后，有如下结论：

当Hopfield网络的神经元传递函数g是连续且有界的，例如Sigmoid函数，并且网络的权系数矩阵对称，则这个连续Hopfield网络是稳定的。在实际应用中，任何一个系统，如果其优化问题可以用能量函数E(t)作为目标函数，那么，总可以用连续Hopfield网络对其进行求解。由于引入能量函数E(t)，Hopfield使神经网络和问题优化直接对应；这种工作是具开拓性的。利用神经网络进行优化计算，就是在神经网络这一动力系统给出初始的估计点，即初始条件；然后随网络的运动传递而找到相应极小点。这样，大量的优化问题都可以用连续的Hopfield网来求解。这也是Hopfield网络用于神经计算的基本原因。

留下评论

You must be logged in to post a comment.