个人技术笔记

【转】超限学习机（Extreme Learning Machine）

发布时间：2016-10-07  栏目：人工智能, 机器学习, 深度学习  评论：0 Comments

1. ELM 是什么

ELM的个人理解： 单隐层的前馈人工神经网络，特别之处在于训练权值的算法: 在单隐层的前馈神经网络中，输入层到隐藏层的权值根据某种分布随机赋予，当我们有了输入层到隐藏层的权值之后，可以根据最小二乘法得到隐藏层到输出层的权值，这也就是ELM的训练模型过程。

与BP算法不同，BP算法（后向传播算法），输入层到隐藏层的权值，和隐藏层到输出层的权值全部需要迭代求解（梯度下降法）

 

 

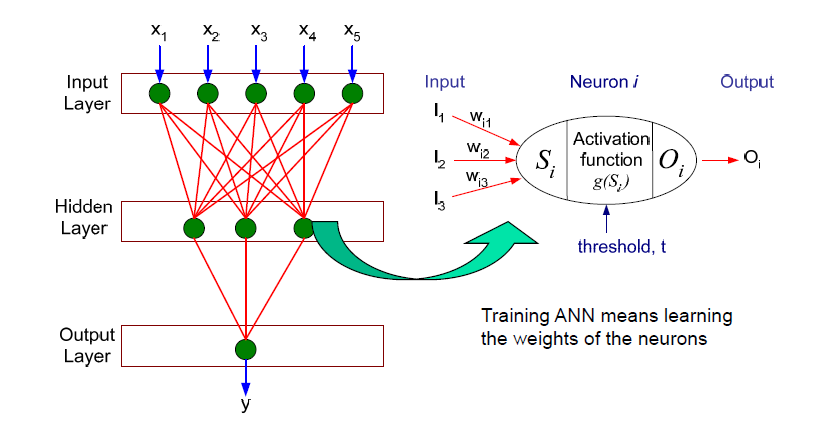
用一张老图来说明，也就是说上图中的Wi1,Wi2,Wi3 在超限学习机中，是随机的，固定的，不需要迭代求解的。我们的目标只需要求解从隐藏层到输出层的权值。毫无疑问，相对于BP算法，训练速度大大提高了。

 

 

2. ELM 的训练过程

 

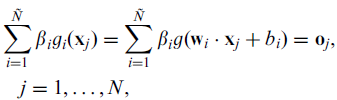
在上述公式中，w_i 表示输入层到隐藏层的权值， b_i表示系统偏置(bias)，ß   则是我们的目标：隐藏层到输出层的权值，N 表示训练集的大小，o_j 表示分类结果。为了无限逼近训练数据的真实结果，我们希望分类结果与真实结果t一致，那么也就是所以上式可以表示为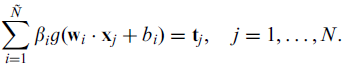 (懒了，不想用公式编辑器，TAT)

用矩阵表示，则 

其中N 表示训练集的大小，N~ 表示隐藏层结点的数量，g(x)表示active function（激活函数？），g(x)要求无限可微。

怎么求解这个方程就成为了ELM的训练过程，恩。

求解方法：1. 传统的梯度下降法 （不说了，就是BP算法）

2.  LS 最小二乘法方法

目标：最小化误差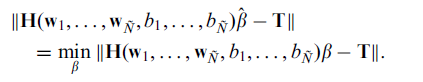

根据 Hß = T， 如果H 是一个方阵的话，ß可以直接求解为H^-1T。

如果H不是， 最小误差的ß 为 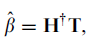，其中H⁺ 为H的Moore-Penrose 广义逆。

留下评论

You must be logged in to post a comment.