【转】Understanding Locally Connected Layers In Convolutional Neural Networks
发布时间：2017-03-21 栏目：机器视觉 评论：0 Comments
Convolutional Neural Networks (CNNs) have been phenomenal in the field of image recognition. Researchers have been focusing heavily on building deep learning models for various tasks and they just keeps getting better every year. As we know, a CNN is composed of many types of layers like convolution, pooling, fully connected, and so on. Convolutional layers are great at dealing with image data, but there are a couple of restrictions as well. The DeepFace network built by Facebook used another type of layer to speed up their training and get amazing results. This layer is called Locally Connected Layer with unshared weights. So what exactly does it do that other layers can’t?
Fully connected and convolutional layers
Before we start discussing locally connected layers, we need to understand where it comes from. Back when neural networks started gaining traction, people were heavily into fully connected layers. It’s basically connected all the neurons in one layer to all the neurons in the next layers. Let’s see what a fully connected and convolutional layers look like:
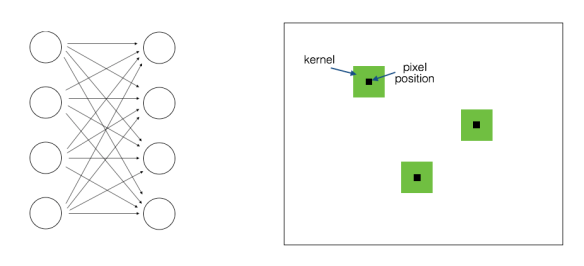
The one on the left is the fully connected layer. The figure on the right indicates convolutional layer operating on a 2D image. This gives a lot of freedom for the neural network to train and optimize all the parameters. But at the same time, it’s computationally intensive! So in order to take advantage of the 2D structure of image data, researchers came up with convolutional layers.
On each 2D array of data, we train a whole bunch of N x N kernels. These kernels are nothing but filters that we run across the 2D array. For each position (x,y), we compute the dot product summation between this kernel and the image values around that point. This process is called convolution, hence the name convolutional neural networks. As we can see in the image above, the kernels will remain the same everywhere (as indicated by the green color).
We’re like half way through and we still haven’t talked about “locally connected” layers
Well, that’s not exactly true! Convolutional layers are technically locally connected layers. To be precise, they are locally connected layers with shared weights. We run the same filter for all the (x,y) positions in the image. In other words, all the pixel positions “share” the same filter weights. We allow the network to tune the filter weights until we arrive at the desired performance. While this is great at image classification tasks, we tend to miss out on some subtle nuances of spatial arrangements.
So researchers tried out an approach where they have a different filter for each (x,y) position. There’s no convolution as such! It’s just a dot product at each pixel position. Let’s say we want train 256 filters of size 5×5 at the current stage of the network.Here, each filter learns to detect different aspects of the image. The input image is of size, say, 128 x 128. We can fit 124 x 124 filters in that image grid (draw it on a piece of paper to verify). As seen from the figure to the left, the different colors indicate different filters. In a convolutional layer, we just need to train 5 x 5 x 256 number of parameters. But if we are dealing with locally connected layers with unshared weights, we will be dealing with 5 x 5 x 256 x 124 x 124.
That’s a lot of parameters
Now you might think — Won’t that result in an enormous number of hyperparameters? Because we are building a separate filter for each pixel position and there are a lot of positions in the image. The answer is yes! But they have optimized the methods and created a fast implementation on the GPU. Also, since every pixel position gets its own filter, they reduce the number of overall filters that need to be trained. The locally connected layers with unshared weights seemed to work well for the DeepFace architecture. It is yet to undergo rigorous testing to see if it can generalize well for other types of image recognition tasks.
In essence, this layer is just like a convolutional layer in the deep neural network, but without any sharing of weights. If you keep this fact aside, it’s pretty much the same as a convolutional layer.
留下评论
You must be logged in to post a comment.
