蒙特卡洛树搜索（MCTS）
发布时间：2020-02-26 栏目：人工智能, 强化学习 评论：0 Comments
Black box optimization基础
了解完Game theory，第二个需要了解的是Black box optimization，也就是黑盒优化。我们知道优化就是根据给定的数据集找到更好的选择，例如机器学习就是典型的优化过程，但我们用的机器学习算法如LR、SVM、DNN都不是黑盒，而是根据数学公式推导通过对函数求导等方式进行的优化。如果我们能把问题描述成一个函数或者凸优化问题，那么我们通过数学上的求导就可以找到最优解，这类问题并不需要用到MCTS等搜索算法，但实际上很多问题例如围棋就无法找到一个描述输赢的函数曲线，这样就无法通过纯数学的方法解决。
这类问题统称为黑盒优化问题，我们不能假设知道这个场景内部的函数或者模型结构，只能通过给定模型输入得到模型输出结果来优化。例如多臂laohu机（Multi-arm Bandit）问题，我们有多台laohu机可以投币，但不知道每一台输赢的概率，只能通过多次投币来测试，根据观察的结果预估每台机器的收益分布，最终选择认为收益最大的，这种方法一般会比随机方法效果好。
黑盒优化的算法也有很多，例如进化算法、贝叶斯优化、MCTS也算是，而这些算法都需要解决如何权衡探索和利用（Exploration and Exploitation）的问题。如果我们只有一个投币，那么当前会选择期望收益最高的laohu机来投（Exploitation），但如果我们有一万个投币，我们不应该只投一个laohu机，而应该用少量币来探索一下其他laohu机（Exploration），说不定能跳过局部最优解找到更优解，当然我们也不能全部投币都用来探索了。
————————————
应用于下棋等一连串的动作中去，第一部随机选取，针对随机选取的结果，随机进行完所有步骤（模拟），再根据模拟结果是否完成（赢或者输），反向返回给这一步一个reward，这样模拟指定次数之后，采样到一定的概率，进而进行判断是否要进行这一步。
—————————————————————————
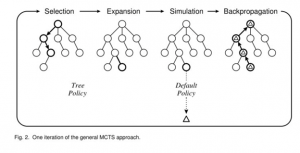
模拟是一个移动的序列，从当前节点开始，到终端节点结束。也就是从当前游戏状态开始，一直玩玩玩（按照某种随机方式），玩到游戏分出胜负位置，从此当前到游戏结束每一步怎么下的序列。
那么，如何在模拟中如何选择移动呢？模拟中移动的选择是依据叫做rollout策略的函数。即根据当前游戏状态产生下一个移动。实际应用中，rollout策略往往会被设计成快速的，从而能够快速进行多次模拟，默认的rollout策略函数是均匀随机分布。
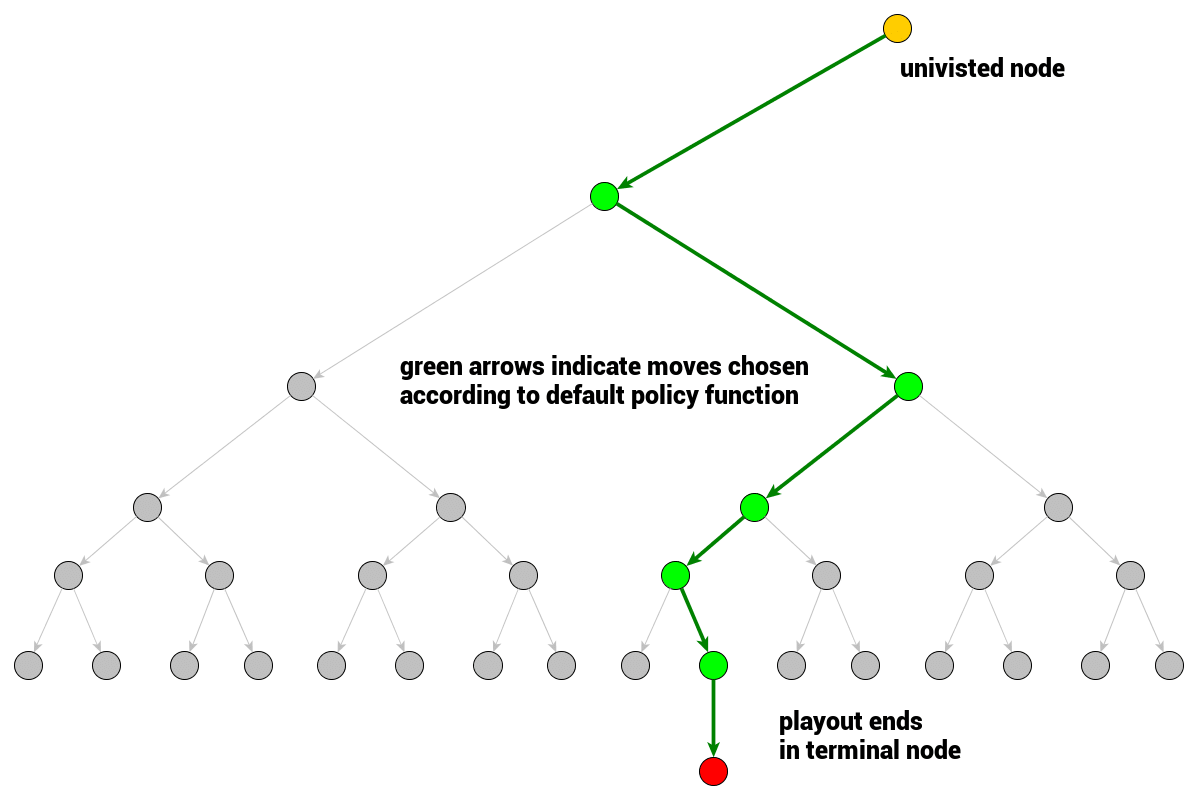
游戏树节点扩展——完全扩展和访问过的节点
先来让我们思考一下人类是如何进行围棋或国际象棋的。
给定一个根节点和游戏的规则，剩下的游戏树就可以推导出来了，所以我们可以不用将整个树都保存到内存中。在初始状态，我们位于游戏树的根节点，其他的节点都是未访问的。一旦我们考虑 一步移动，就会想象这个动作会产生什么样的结果。
MCTS也是一样，节点分为访问过的和未访问过的。被访问过的节点意味着某个模拟过程是以它为起点的，即它至少被评估过一次。如果一个节点的所有子节点都被访问过了，那这个节点就称为是完全扩展的，否则就是未完全扩展的。
反向传播
当完成对一个节点的模拟，其结果已准备好传播回当前游戏树的根节点，然后模拟开始的节点被标记为已访问。
树的置信度上界（Upper Confidence Bound applied to Trees，UCT）。
UCT是一个让我们从已访问的节点中选择下一个节点来进行遍历的函数，也是MCTS的核心函数。
MCTS的终止
现在，我们知道了成功实现MCTS的必要条件，但是仍有几个问题我们需要回答。首先，我们应该什么时候结束MCTS过程？答案是：它取决于上下文。如果你考虑搭建一个游戏引擎，那么你的“思考时间”可能是有限的，计算能力也是有限的。因此最保险的做法是在你资源允许的情况下尽可能久地运行MCTS。
当MSCT程序结束时，最佳的移动通常是访问次数最多的那个节点。
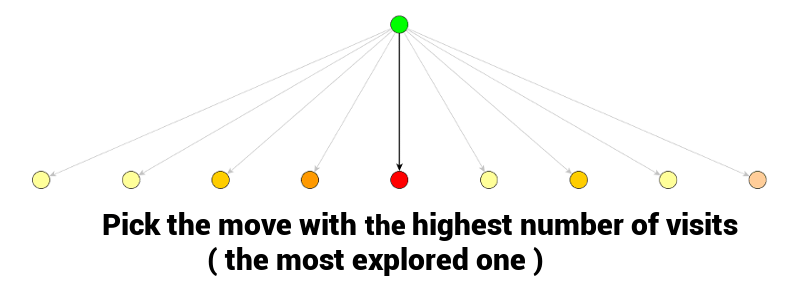
当你使用MCTS选择了移动之后，你选择的节点将变成你对手移动的游戏状态。当你对手选择了他的移动，你将再次从对手选择的节点处开始MCTS搜索。先前MCTS的一些统计信息可能仍然存在于你在正在考虑的新分支中，这样就可以不用重新构建树而是重用统计数据即可。
—————————————————–
参考：https://blog.csdn.net/qq_16137569/article/details/83543641
